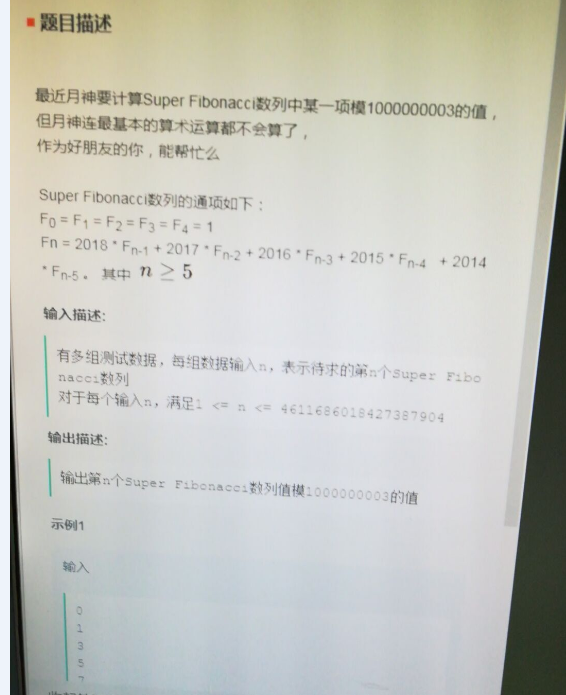
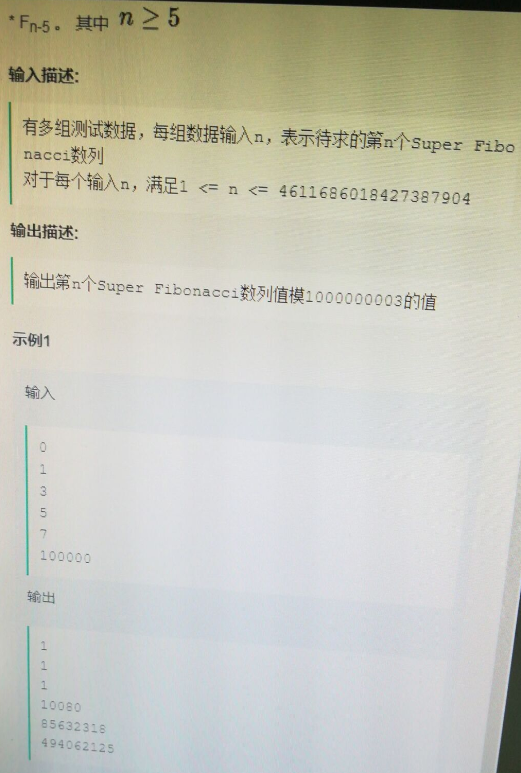
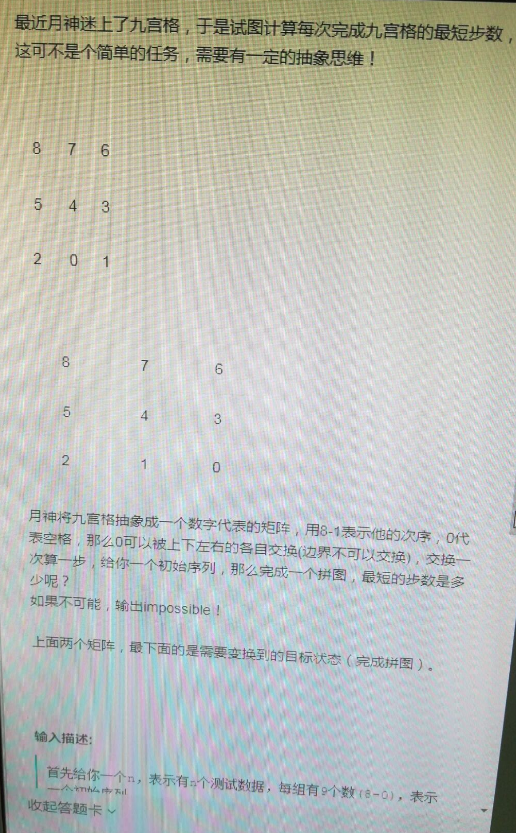
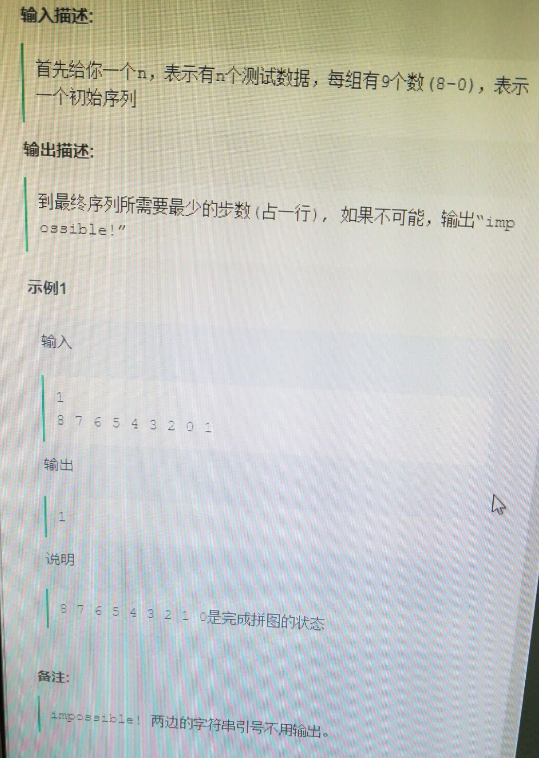
// 第二题O(n)空间#if 0typedef long long ll;int main(){ ll n; while (cin >> n) { if (n < 5) { cout << 1 << endl; continue; } vector dp(n + 1); dp[0] = dp[1] = dp[2] = dp[3] = dp[4] = 1; for (ll i = 5; i <= n; i++) { dp[i] = 2018 * dp[i - 1] % 1000000003 + 2017 * dp[i - 2] % 1000000003 + 2016 * dp[i - 3] % 1000000003 + 2015 * dp[i - 4] % 1000000003 + 2014 * dp[i - 5] % 1000000003; } cout << dp[n] % 1000000003 << endl; } return 0;}#endif// 第二题 时间复杂度超时#if 0typedef long long ll;inline ll ksc(ll x, ll y, ll mod){ return (x*y - (ll)((long double)x / mod*y)*mod + mod) % mod;}int main(){ ll n; while (scanf("%lld",&n)!=EOF) //while (cin >> n) { if (n < 5) { //cout << 1 << endl; printf("1\n"); continue; } vector dp(6); dp[0] = dp[1] = dp[2] = dp[3] = dp[4] = 1; // 使用6个空间,然后每次都需要移位 for (ll i = 5; i <= n; i++) { dp[5] = 2018 * (dp[4] % 1000000003) + 2017 * (dp[3] % 1000000003) + 2016 * (dp[2] % 1000000003) + 2015 * (dp[1] % 1000000003) + 2014 * (dp[0] % 1000000003); for (int j = 0; j < 5; j++) { dp[j] = dp[j + 1]; } } printf("%lld\n", dp[5] % 1000000003); // 不用移位 //for (ll i = 5; i <= n; i++) //{ // dp[i % 6] = ksc(2018, dp[(i - 1) % 6], 1000000003) + ksc(2017, dp[(i - 2) % 6], 1000000003) + ksc(2016, dp[(i - 3) % 6], 1000000003) + ksc(2015, dp[(i - 4) % 6], 1000000003) + ksc(2014, dp[(i - 5) % 6], 1000000003); // //dp[i % 6] = 2018 * (dp[(i - 1) % 6] % 1000000003) + 2017 * (dp[(i - 2) % 6] % 1000000003) + 2016 * (dp[(i - 3) % 6] % 1000000003) + 2015 * (dp[(i - 4) % 6] % 1000000003) + 2014 * (dp[(i - 5) % 6] % 1000000003); //} ////cout << dp[n%6] % 1000000003 << endl; //printf("%lld\n", dp[n % 6] % 1000000003); } return 0;}#endif// 第二题 时间复杂度超时#if 0typedef long long ll;long long quick_multiply(long long a, long long b, long long mod) { long long result = 0; while (b) { result = (result + (b % 2 * a) % mod) % mod; a = a * 2 % mod; b = b / 2; } return result;}inline ll ksc(ll x, ll y, ll mod){ return (x*y - (ll)((long double)x / mod*y)*mod + mod) % mod;}int main(){ ll n; while (scanf("%lld", &n) != EOF) //while (cin >> n) { if (n < 5) { //cout << 1 << endl; printf("1\n"); continue; } vector dp(6); dp[0] = dp[1] = dp[2] = dp[3] = dp[4] = 1; for (ll i = 5; i <= n; i++) { dp[i % 6] = quick_multiply(2018, dp[(i - 1) % 6], 1000000003) + quick_multiply(2017, dp[(i - 2) % 6], 1000000003) + quick_multiply(2016, dp[(i - 3) % 6], 1000000003) + quick_multiply(2015, dp[(i - 4) % 6], 1000000003) + quick_multiply(2014, dp[(i - 5) % 6], 1000000003); //dp[i % 6] = 2018 * (dp[(i - 1) % 6] % 1000000003) + 2017 * (dp[(i - 2) % 6] % 1000000003) + 2016 * (dp[(i - 3) % 6] % 1000000003) + 2015 * (dp[(i - 4) % 6] % 1000000003) + 2014 * (dp[(i - 5) % 6] % 1000000003); } //cout << dp[n%6] % 1000000003 << endl; printf("%lld\n", dp[n % 6] % 1000000003); } return 0;}#endif#if 0// 快速幂运算求解斐波拉契数列#include #include using namespace std;const int MOD = 10000;struct matrix{ int m[2][2];}ans, base;matrix multi(matrix a, matrix b){ matrix tmp; for(int i = 0; i < 2; ++i) { for(int j = 0; j < 2; ++j) { tmp.m[i][j] = 0; for(int k = 0; k < 2; ++k) tmp.m[i][j] = (tmp.m[i][j] + a.m[i][k] * b.m[k][j]) % MOD; } } return tmp;}int fast_mod(int n) // 求矩阵 base 的 n 次幂 { base.m[0][0] = base.m[0][1] = base.m[1][0] = 1; base.m[1][1] = 0; ans.m[0][0] = ans.m[1][1] = 1; // ans 初始化为单位矩阵 ans.m[0][1] = ans.m[1][0] = 0; while (n) { if (n & 1) //实现 ans *= t; 其中要先把 ans赋值给 tmp,然后用 ans = tmp * t { ans = multi(ans, base); } base = multi(base, base); n >>= 1; } return ans.m[0][1];}int main(){ int n; while (scanf("%d", &n) && n != -1) { printf("%d\n", fast_mod(n)); } return 0;}#endif//计算(x^y) % N; 注:(x^y)表示x的y次方#if 0int main(){ int x, y, N; cin >> x >> y >> N; long res = 1; x = x % N; //开始 while (y > 0) { if (y % 2 == 1) //等价于 if(y&1) res = (res * x) % N; y /= 2; //y>>1; 分解y为二进制编码 x = (x * x) % N; } cout << res << endl; return 0;}#endif